HOMAcalc is end of support. The basic functionalities have been combined into py.Aroma, a multi-functional tool for aromaticity analyses. Please check the homepage of py.Aroma for more information.

Contents

• 1. Background
• 2. Statement of need
• 3. HOMA analyses with HOMAcalc

1. Background

HOMA (Harmonic Oscillator Model of Aromaticity) is a geometry-based aromaticity index. The HOMA model is based on the assumption that the harmonic oscillator energy of extension or compression of a bond depends on the force constants, which are dependent on the bond lengths. HOMA value can be calculated from following equation:

\[{\rm HOMA}=1-\frac {1}{n} \sum^n_i \alpha_j \left( R_{opt,j}-R_{i,j} \right)^2\]

The optimal bond length Ropt is the length of a bond for which equal energy inputs are required to extend it to the length of the singlet bond or to compress it to the length of the double bond. For C-C case, as an example, the Ropt was defined as following:

\[R_{opt}=\frac {1}{3} \left( R_{\rm C-C}+2R_{\rm C=C} \right)\]

Applying C-C bond length (1.467 Å) and C=C bond (1.349 Å) in cyclobuta-1,3-diene, the Ropt of CC bond could be calculated to 1.388 Å. The α is an empirical normalization constant, chosen to give HOMA = 0 for a model nonaromatic system and HOMA = 1 for a system where all bonds are equal to Ropt. α was defined in following equation, where Rs and Rd are bond length for single and double bonds.

\[\alpha = \frac {2}{\left( R_S-R_{opt} \right)^2+\left( R_d-R_{opt}\right)^2}\]

The α and Ropt for common bonds are referred from this paper.

2. Statement of need

HOMAcalc is a Python program for calculating the HOMA in cyclic system easily. About install and usage of HOMAcalc, please refer to the user documents on GitHub.

3. HOMA analyses with HOMAcalc

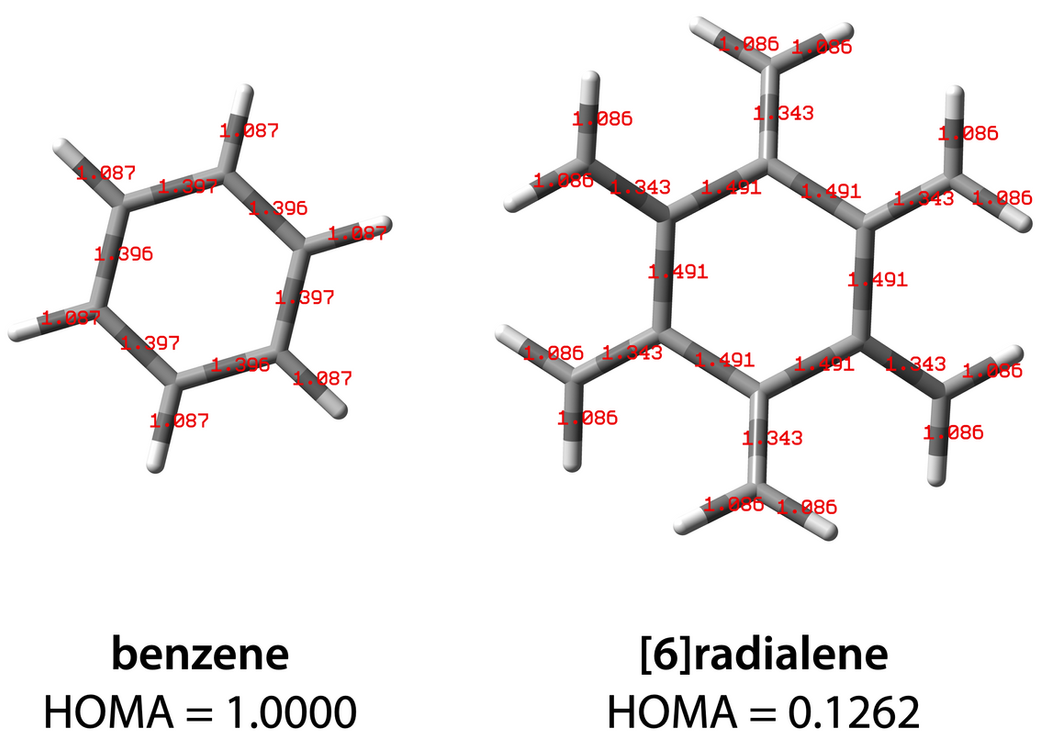
All calculation files could be download from here. Benzene and [6]radialene were optimized at B3LYP/6-31G(d) level of theory, the output files were imported to HOMAcalc, the HOMA values were calculated to be 1 for benzene and 0.13 for [6]radialene.