Computing Charge Transfer Rate Based on Marcus Theory Using Gaussian
1 Preface
This blog is introducing the method for computing charge transfer integral and charge transfer rate constant via Gaussian 16. Here, an open-source program CATNIP would be used, this program could be downloaded freely from the GitHub page.
2 Gaussian Inputs & Outputs
To calculate charge transfer integral between two molecules, three separate calculateions are needed:
- Monomer 1
- Monomer 2
- Dimer
Following keywords should be also included to tell the Gaussian to output the minimized atomic orbital coefficients those are needed for calculating charge transfer integral:
nosymm pop=full iop(3/33=1) punch=mo
You will get a .log file and a Fort.7 file after each calculation. To calculate transfer integral using CATNIP, you need to rename the Fort.7 file to the same name as your .log file with a .pun extension.
3 Charge Transfer Integral
This is just a simple note, for more detail information of how to use CATNIP, please refer to its homepage.
To run a calculation, three .log files and three .pun files are needed, for monomer 1, monomer 2 and dimer, for example:
- 1mer_1.log
- 1mer_1.pun
- 1mer_2.log
- 1mer_2.pun
- 2mer.log
- 2mer.pun
To calculate the charge transfer integral for the HOMO between the monomers, run following command (Note that the .log files and .pun files should be located in the same folder):
calc_J -p_1 1mer_1.pun -p_2 1mer_2.pun -p_P 2mer.pun
To calculate the charge transfer integral for the LUMO, the orbital types must be specified:
calc_J -p_1 1mer_1.pun -orb_ty_1 LUMO -p_2 1mer_2.pun -orb_ty_2 LUMO -p_P 2mer.pun
The effective (or generalized) charge transfer integral J_eff (also known as electronic coupling V) would be shown on the screen:
J_eff -0.00190564 eV
4 Charge Transfer Rate Constant Based on Marcus Theory
By Marcus theory, the rate constant of charge transfer k_et could be computed from electronic coupling V (J_eff) and reorganization energy λ:
\[k_{\rm et} = \sqrt { \frac {\pi}{\lambda k_{\rm B}T}} \frac{V^2}{\hbar} \exp {\left( - \frac {\lambda}{4k_{\rm B}T} \right)}\]where, reduced Planck constant ħ, Boltzmann constant k_B, temperature T are also needed.
The reorganization energy λ is defined as the energy difference between the charged and neutral systems at the two different geometries (adiabatic potential energy surface). To compute it, four separated calculations are needed, e.g. for eletron transfer:
- Geometry optimizaiton of neutral state (E_1)
- Single point calculation of anion state with neutral geometry (E_4)
- Geometry optimizaiton of anion state (E_3)
- Single point calculation of neutral state with anion geometry (E_2)
and the reorganization energy is:
\[\lambda = \lambda_1 + \lambda_2\] \[\lambda_1 = E_2 - E_1\] \[\lambda_2 = E_4 - E_3\] 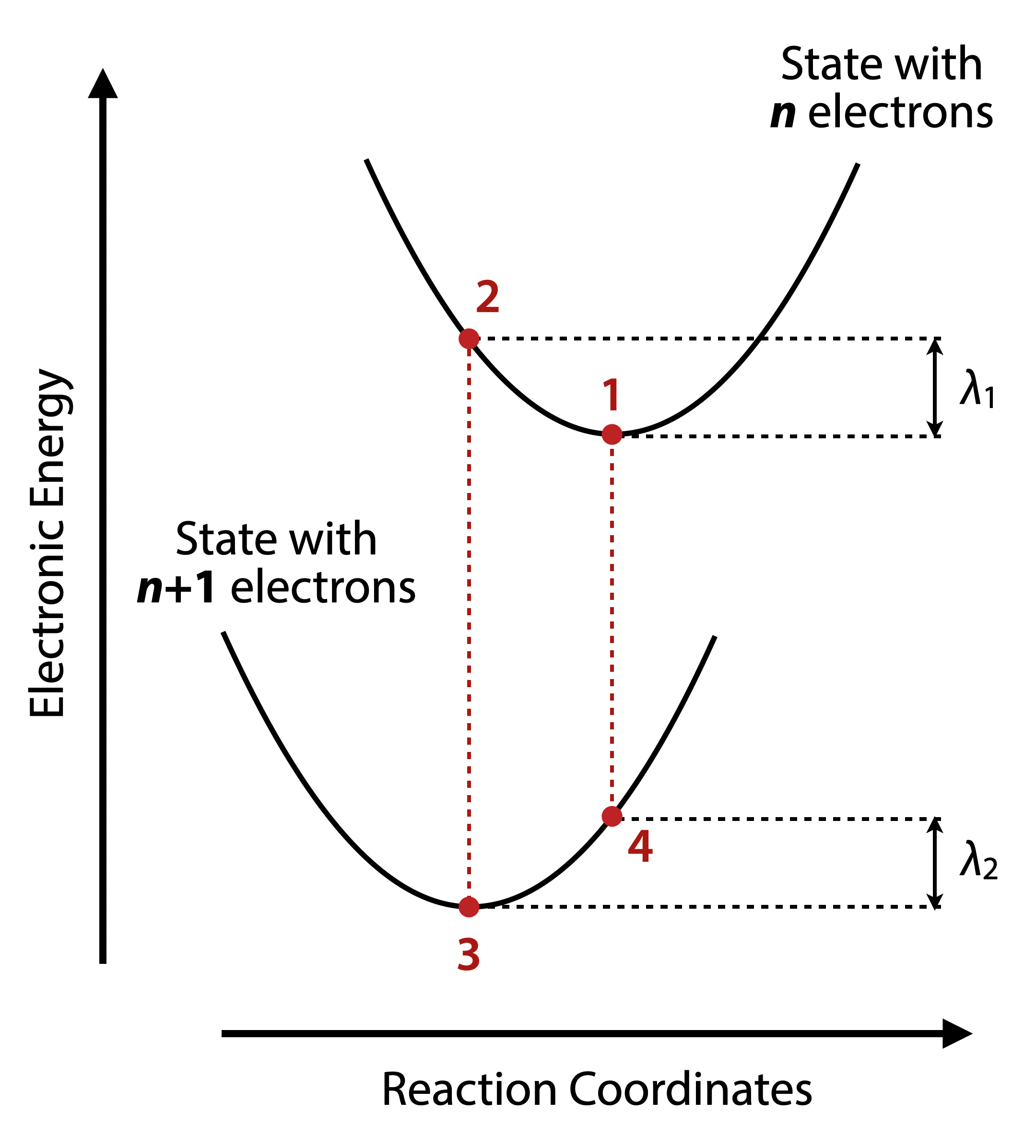
Here I provided an Excel tool for computing the λ and k_et based on Marcus theory, download from here.
5 Example
Here is an example for a naphthalene dimer, the Cartesian coordinates were obtained from ADF official tutorials page. All files could be downloaded from here.
Monomer 1:
%nprocshared=8
%mem=10GB
# pw91pw91/tzvp nosymm pop=full iop(3/33=1) punch=mo
naphthalene monomer 1
0 1
C -2.96292735 -1.37776232 2.34412329
H -3.91358911 -3.24557560 2.36511160
C -2.19933829 -0.51291048 1.59118541
C -1.08607265 -1.59873768 -2.34412329
C -2.23157919 -2.11438654 -0.26513808
C -1.81742081 -0.86211346 0.26513808
H -2.14645018 -3.30748680 -1.93535091
H -0.80423336 -1.83888170 -3.25104686
H -0.76084457 0.83758710 -0.16847761
C -3.01509821 -2.98739399 0.54127003
H -3.28815543 -3.81408710 0.16847761
H -3.24476664 -1.13761830 3.25104686
C -1.03390179 0.01089399 -0.54127003
H -1.90254982 0.33098680 1.93535091
C -3.37590246 -2.62057013 1.81755935
C -0.67309754 -0.35592987 -1.81755935
H -0.13541089 0.26907560 -2.36511160
C -1.84966171 -2.46358952 -1.59118541
Monomer 2:
%nprocshared=8
%mem=10GB
# pw91pw91/tzvp nosymm pop=full iop(3/33=1) punch=mo
naphthalene momomer 2
0 1
C 2.96292735 1.59873768 -2.34412329
C 1.08607265 1.37776232 2.34412329
C 1.84966171 0.51291048 1.59118541
H 1.90254982 3.30748680 -1.93535091
C 2.19933829 2.46358952 -1.59118541
C 2.23157919 0.86211346 0.26513808
C 1.03390179 2.98739399 0.54127003
C 1.81742081 2.11438654 -0.26513808
C 0.67309754 2.62057013 1.81755935
H 3.28815543 -0.83758710 -0.16847761
H 0.80423336 1.13761830 3.25104686
C 3.01509821 -0.01089399 -0.54127003
H 2.14645018 -0.33098680 1.93535091
H 3.91358911 -0.26907560 -2.36511160
H 0.76084457 3.81408710 0.16847761
C 3.37590246 0.35592987 -1.81755935
H 3.24476664 1.83888170 -3.25104686
H 0.13541089 3.24557560 2.36511160
Dimer:
%nproc=8
%mem=10GB
# pw91pw91/tzvp nosymm pop=full iop(3/33=1) punch=mo
naphthalene dimer
0 1
C -2.96292735 -1.37776232 2.34412329
H -3.91358911 -3.24557560 2.36511160
C -2.19933829 -0.51291048 1.59118541
C -1.08607265 -1.59873768 -2.34412329
C -2.23157919 -2.11438654 -0.26513808
C -1.81742081 -0.86211346 0.26513808
H -2.14645018 -3.30748680 -1.93535091
H -0.80423336 -1.83888170 -3.25104686
H -0.76084457 0.83758710 -0.16847761
C -3.01509821 -2.98739399 0.54127003
H -3.28815543 -3.81408710 0.16847761
H -3.24476664 -1.13761830 3.25104686
C -1.03390179 0.01089399 -0.54127003
H -1.90254982 0.33098680 1.93535091
C -3.37590246 -2.62057013 1.81755935
C -0.67309754 -0.35592987 -1.81755935
H -0.13541089 0.26907560 -2.36511160
C -1.84966171 -2.46358952 -1.59118541
C 2.96292735 1.59873768 -2.34412329
C 1.08607265 1.37776232 2.34412329
C 1.84966171 0.51291048 1.59118541
H 1.90254982 3.30748680 -1.93535091
C 2.19933829 2.46358952 -1.59118541
C 2.23157919 0.86211346 0.26513808
C 1.03390179 2.98739399 0.54127003
C 1.81742081 2.11438654 -0.26513808
C 0.67309754 2.62057013 1.81755935
H 3.28815543 -0.83758710 -0.16847761
H 0.80423336 1.13761830 3.25104686
C 3.01509821 -0.01089399 -0.54127003
H 2.14645018 -0.33098680 1.93535091
H 3.91358911 -0.26907560 -2.36511160
H 0.76084457 3.81408710 0.16847761
C 3.37590246 0.35592987 -1.81755935
H 3.24476664 1.83888170 -3.25104686
H 0.13541089 3.24557560 2.36511160
The command used for CATNIP:
calc_J -p_1 naph_mol1.pun -orb_ty_1 LUMO -p_2 naph_mol2.pun -orb_ty_2 LUMO -p_P naph_p.pun
and here is the output:
Running calc_J VERSION 1.9
log file for first monomer is: naph_mol1.log
log file for second monomer is: naph_mol2.log
log file for dimer is: naph_p.log
pun file for the first monomer is: naph_mol1.pun
pun file for the second monomer is: naph_mol2.pun
pun file for the dimer is: naph_p.pun
Dimer Spin Alpha
Monomer 1 Spin Alpha Orbital LUMO
Monomer 2 Spin Alpha Orbital LUMO
J_ab -0.0558655 eV
e_a -1.88656 eV
e_b -2.14962 eV
S_ab 0.00943935
J_eff -0.0368193 eV
For comparsion, the J_eff calculated at same level of theory by ADF was -0.03780 eV.
FYI:
\[V = J_{\rm eff} = \frac{J_{\rm ab} - \frac{S_{\rm ab}(e_{\rm a} + e_{\rm b})}{2}}{1-S_{\rm ab}^2}\] \[\hbar = 1.054571817 \times 10 ^ {-34} \, \rm {J \cdot s} = 6.582119569 \times 10 ^{-16} \, \rm {eV \cdot s}\] \[k_{\rm B} = 1.380649 \times 10 ^ {-23} \, \rm {J \cdot K^{-1}} = 8.617333262 \times 10 ^{-5} \, \rm {eV \cdot K^{-1}}\] \[1 \, {\rm eV} = 1.60218 \times 10 ^ {-19} \, {\rm J}\] \[1 \, {\rm J} = 6.24151 \times 10 ^ {18} \, {\rm eV}\]The reorganization energy λ was computed to 0.23 eV, thus, the k_et for electrons is 4.85E+12 / s at 300 K.
Enjoy Reading This Article?
Here are some more articles you might like to read next: